Calculus: Limits

LIMITS

 

 

INTRODUCTION

 

 

 

 

In mathematics, a limit is the value that a function or sequence "approaches" as the input or index approaches some value. Limits are essential to calculus (and mathematical analysis in general) and are used to define continuity, derivatives, and integrals.

 

 

EXPLANATION

 

Suppose f is a real-valued function and c is a real number. Intuitively speaking, the expression

${\displaystyle \lim _{x\to c}f(x)=L}$

means that f(x) can be made to be as close to L as desired by making x sufficiently close to c. In that case, the above equation can be read as "the limit of f of x, as x approaches c, is L".



EXAMPLE

1. Replacing the value of x by its tendency (when x tends to a number)
(x² − 1) (x − 1)
Let's work it out for x=1:

(1² − 1) (1 − 1) = (1 − 1) (1 − 1) = 0 0 

 

 

2. Factoring

By factoring (x2−1) into (x−1)(x+1) we get:
Now we can just substitiute x=1 to get the limit:

 

 

3. Conjugate

 

When it's a fraction, multiplying top and bottom by a conjugate might help.

 

Evaluating this at x=4 gives 0/0, which is not a good answer!

So, let's try some rearranging:

Multiply top and bottom by the conjugate of the top:
Simplify top using :
Simplify top further:
Cancel (4−x) from top and bottom:

So, now we have:

 

 

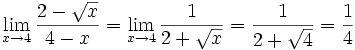
VIDEO

 

 

Here is a video for you to understand better this topic

 



 

 

PRACTICE

 

1.  

[Solution]

2.  

[Solution]

3.  

[Solution]   

 

GOOD LUCK AND HOPE YOU HAVE UNDERSTOOD!!